12月6日至12日,14位诺贝尔奖获奖者齐聚斯德哥尔摩,参与为期一周的2025年诺贝尔颁奖周活动。获奖者涵盖生理学或医学奖、物理学奖、化学奖及经济学奖等多个领域。继今年10月受邀参加诺贝尔奖新闻发布会后,墨子沙龙再次荣幸获邀参与本届诺奖周活动。在卡洛琳斯卡医学院和瑞典皇家科学院,墨子沙龙现场参加了诺贝尔奖得主记者见面会,聆听了获奖者们的学术报告,并将陆续与读者分享现场的精彩内容。
Michel H. Devoret(米歇尔·德沃雷特),1982年博士毕业,法国物理学家,耶鲁大学应用物理学教授,量子电路理论奠基人之一。他在诺奖这为大家带来了题为《从宏观量子现象到人工原子》(“From Macroscopic Quantum Phenomena to Artificial Atoms”)的报告。
从α衰变到宏观量子效应
今年是量子力学诞生一百周年,我在这里演讲感到格外荣幸。我们认为量子力学与直觉相悖,它的逻辑与我们日常生活中所体验到的逻辑截然不同。在我攻读博士学位时,曾将量子力学应用于一个简单的分子——氢分子。
40年前我在
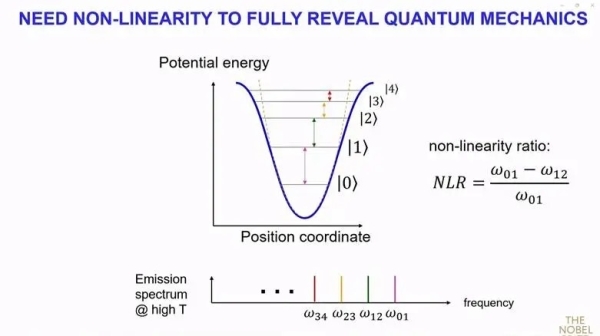
如果想要控制和操控系统,必须要控制非线性和损耗。因为关键在于两个峰值之间的相对距离与宽度的关系。你需要一个良好的非线性系统,但同时又需要极低的损耗。托尼·拉加德意识到了这一点。目前只有约瑟夫森隧道元件能够同时提供极低的损耗和足够的非线性。
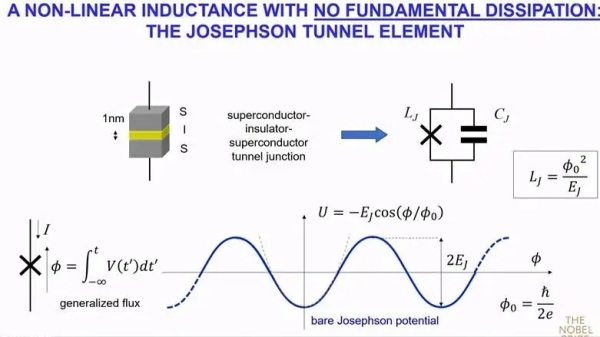
在电路图中用十字形元件代替了电感器,代表约瑟夫森隧道元件。十字形元件本身并不代表电感,但选择十字形元件是由于约翰·斯托克(John Stock)的理论,它将电流与磁通量联系起来。由于磁通量对时间导数等于电压,引入节点两端电压的时间积分,得到的变量是磁通量。
约翰·克拉克(John Clarke)实验室做博士后时受到很多启发。我和当时还是研究生的约翰·马丁尼斯(John
Martinis)一起开始了一项实验,我们尝试用量子力学领域中解释我们测试的电流和电压。在当时,微观标量尺度的量子力学并非完全是新概念,并且可以在量子力学的科普书籍中看到相关内容。
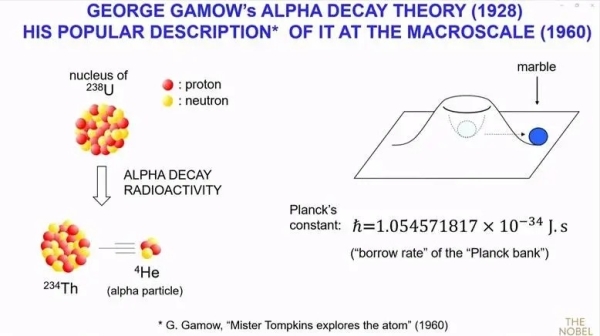
我举一个例子,乔治·伽莫夫(George Gamow)的书——《汤普金斯先生探索原子世界》(Mister Tompkins explores the atom)。他在量子力学发现后不久,就通过以下概念解释了α衰变和α放射性。例如,以铀原子为例,它的原子核经过一段时间后会衰变成钍(Th),并释放出一个α粒子,它实际上是一个氦原子,或者也可以理解为两个质子和两个中子。如果用γ射线来描述α粒子,可以被比作一颗弹珠。这颗弹珠最初位于一个中间有陨石坑的小土堆中。如果用经典力学来描述这颗弹珠,它无法逃逸,因为能量不守恒。它必须先在土堆上并且上下移动才能逃逸。
但从量子力学的角度来看,这颗弹珠可以利用普朗克能量库(Plank bank)的能量。普朗克能量库规定了你可以在很短的时间内“借用”一定量的能量。实际上,这个能量是由普朗克常数决定的。普朗克常数告诉我们,在1秒内你可以“借用”10^-34焦耳的能量,或者在1纳秒内“借用”10^-25焦耳的能量。而且,土堆的凹陷对应于原子核内部α粒子的强相互作用力,这就是你会看到凹陷的原因。但是,在原子核外部,带正电的α粒子受到原子核的排斥,因此呈现出向下倾斜的势垒。所以,这个势垒可以用γ射线来描述α衰变。如果你拿一个家里的狗碗和一颗弹珠,只要弹珠足够轻,你就能看到这种神奇的现象。
实际上,我们完全没有证据表明量子力学在宏观上有效,尽管当时人们认为超流体或超导现象在微观尺度上展示了量子力学的规律,但在这些现象中,量子关联实际上是在极小的尺度上发挥作用的,这种有序性在微观尺度上是通过完全经典的相互作用传播的。当一只猫同时处于“死”和“活”的叠加态时,当叠加态发生变化时,测量结果也会随之改变,最终只有一个结果:猫要么是死的,要么是活的。类比在电路上:电子振荡器,它由尺寸约为毫米级的铝制成。如果将其冷却到2000万开尔文,电路中的所有电子都会凝聚成一种不可压缩的流体,并在电路中快速运动。
为了理解电路的微观特性,我们可以将其与原子进行比较。以氢原子为例,氢原子中只有一个电子,等效于一个由电感器和电容器并联而成的电路。在这个系统中,电子会从电容器的一侧极板快速移动到另一侧极板。在经典的理论模型中,电子围绕质子运行,那么在电路中发生了什么呢?电路中的不可压缩的流体会通过电感器带动电容器的极板移动,但是在低温下这种运动实际上并没有激发任何内部自由度。在原子中只有一个电子。类比在电路中,则是一个完整的超导体。当把凝聚体的质心比作电子的位置。电子的速度就是流过电感器的电流,而作用在电子上的力相当于电容器上的电压。
如果想要控制和操控系统,必须要控制非线性和损耗。因为关键在于两个峰值之间的相对距离与宽度的关系。你需要一个良好的非线性系统,但同时又需要极低的损耗。托尼·拉加德意识到了这一点。目前只有约瑟夫森隧道元件能够同时提供极低的损耗和足够的非线性。
在电路图中用十字形元件代替了电感器,代表约瑟夫森隧道元件。十字形元件本身并不代表电感,但选择十字形元件是由于约翰·斯托克(John Stock)的理论,它将电流与磁通量联系起来。由于磁通量对时间导数等于电压,引入节点两端电压的时间积分,得到的变量是磁通量。
通过处理积分我们得到具有周期性的余弦势,它由 ħ/2e 给出。由于在超导态下,电子会成对地隧穿,所以在上式用到了电子e。是什么决定了这个势的形状?电荷一个一个地穿过结形成周期性变化。由于不等距的能级测量起来实际上非常困难。所以,我们在实验上施加一个偏置电流,当电流穿过结会使余弦势发生倾斜。现在,我们有了这些能级,但它们是亚稳态的。如果你占据其中一个能级,波函数会泄漏到势垒会产生衰变。有两个参数决定了这个势能还有频率ωp,它是势阱底部微小振荡的频率,以及势垒高度。在实验中,为什么控制这两个参数至关重要呢?势阱的状态有两种逃逸机制,黄色小球表示的是整个势阱的状态。它可以从势阱逃逸到任何过程中。由于热激发,黄色小球可以从一个能级跃迁到下一个能级,直到从势垒顶部逃逸出来。如果现在温度很低,粒子就会通过隧穿效应穿过势垒逃逸,这种情况就类似于α衰变。
我们整个电路现在相当于一个放射性原子核,如何检测这种放射性呢?在这个系统中,偏置电流通过隧穿元件,通过对应于黄色粒子的十字形结构对应于电路的状态,代表粒子被捕获。粒子可以在电路中移动,但它的平均速度为零,对应电容两端的电压为零。当我们引入一个电阻,它相当于电压表。当整个电路的状态从零电压状态切换到非零电压状态时,电压表的作用相当于放射性衰变中的盖革计数器,我们称为电压状态。粒子一旦逃逸,就会沿着倾斜的电势垒向下滚动,当速度不断增加就会产生电压,就可以用电压表检测。通过检测电压脉冲,就可以知道整个电路的状态,对应于微观层面的α衰变。
在这个实验中,单个电子穿过势垒的隧穿效应会产生约瑟夫森效应,这种隧穿效应与整个电路从一种电流切换到另一种电流无关。这两种隧穿效应不应混淆。所以我们发现的是整个电路状态的隧穿、电子的隧穿以及成对电子的隧穿,这是约瑟夫森的发现,而我们所做的是后约瑟夫森物理学。
我们利用铌制成的结,它在氦温度下具有超导性所以我们可以检查所有参数。圆柱体是滤波器,我们将带宽缩小到千赫兹,并且滤除频谱中的其他部分。测量等离子体频率非常重要,因为它决定了交叉温度。我们在经典状态下进行的一项实验告诉我们,如果我们测量隧穿效应,就可以在共振曲线的右边缘找到等离子体频率。之前的这些实验开启了量子超导电路这个新领域,在这个领域中,它们可以组合起来制造人造原子、分子,甚至是更复杂的电路,例如量子极限放大器。
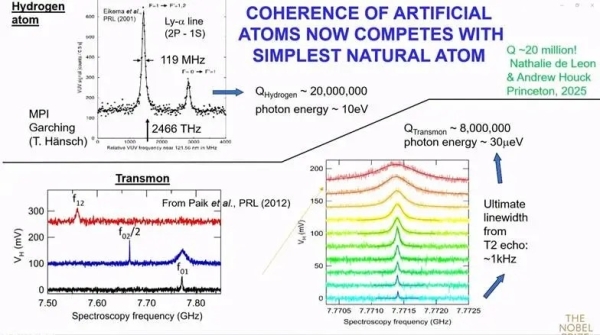
在此,我要感谢在座各位参与了这项探索。这些人工原子拥有类似于曼德拉效应表的结构。其中两种比较流行的是“传输子(Transmon)”和“磁通子(Fluxonium)”。在娜塔莉·德莱昂 (Natalie De Leon)和安德鲁·凯特·普林斯顿(Andrew Kate Princeton)的团队中,这些人工原子的性质已经扩展到了原子数量级,基本上与氢原子相当。这些人工原子能进行一些真实原子无法实现的实验。从长远来看,人工原子物理和微波量子光学这一新兴领域为量子信息处理和量子传感开辟了新的应用前景。
所以,我们还能将这项技术拓展到什么程度?我们究竟能在多大程度上将量子力学推广到微观系统?尽管我们已经将尺度推向了另一个层面,但是这仍然是一个悬而未决的问题。感谢大家的聆听。
